In the world of statistics, understanding how to interpret data effectively is crucial. The Z score calculator is a powerful tool that helps you determine how a particular data point relates to the mean of a dataset. Whether you’re a student, researcher, or data analyst, mastering this tool can significantly enhance your data analysis skills.
Key Takeaways
- The Z score calculator is essential for understanding data variance and standard deviation.
- It helps in comparing different datasets and identifying outliers.
- Knowing how to use the Z score calculator can improve your statistical analysis and decision-making.
Understanding the Z Score

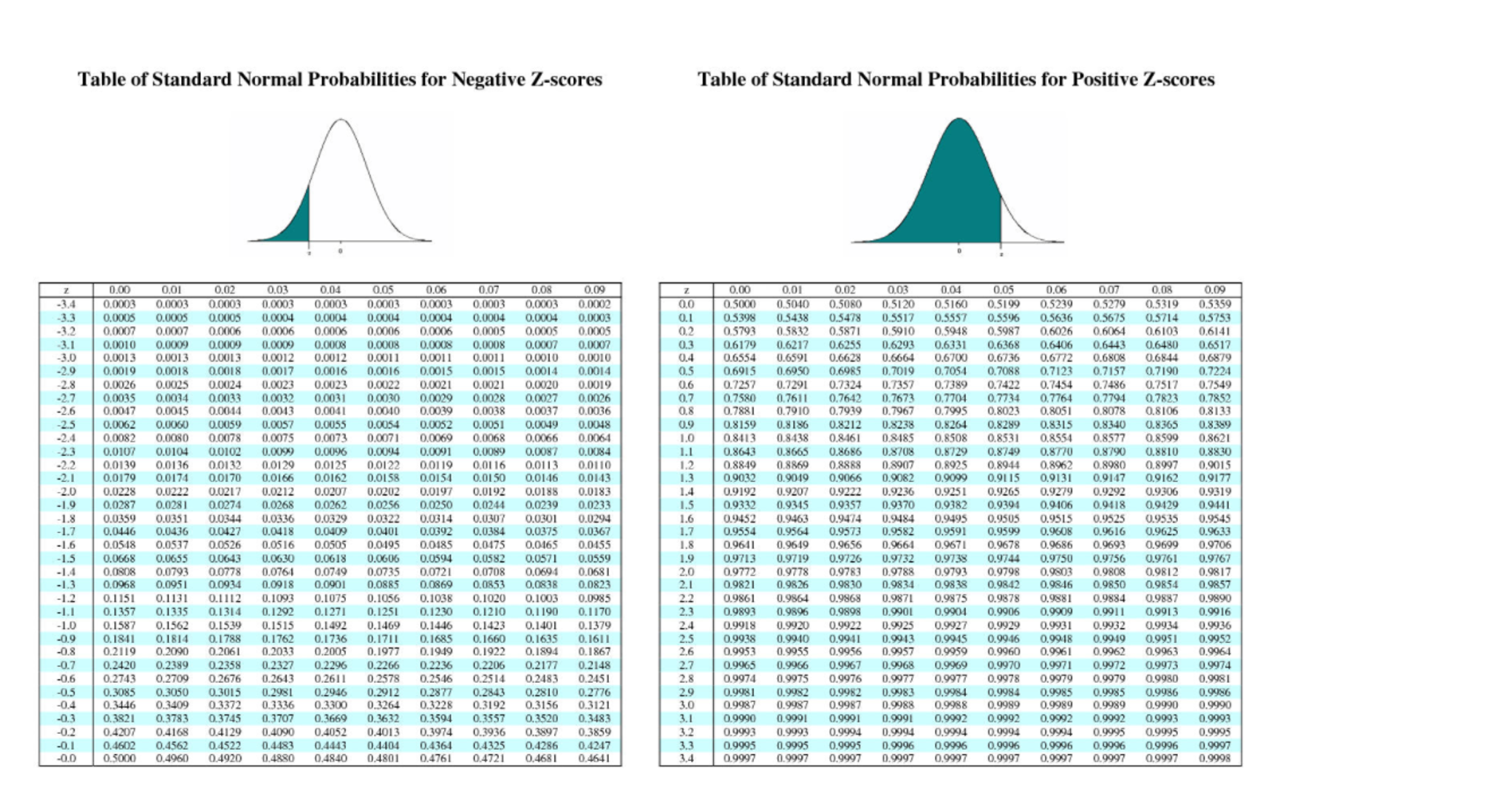
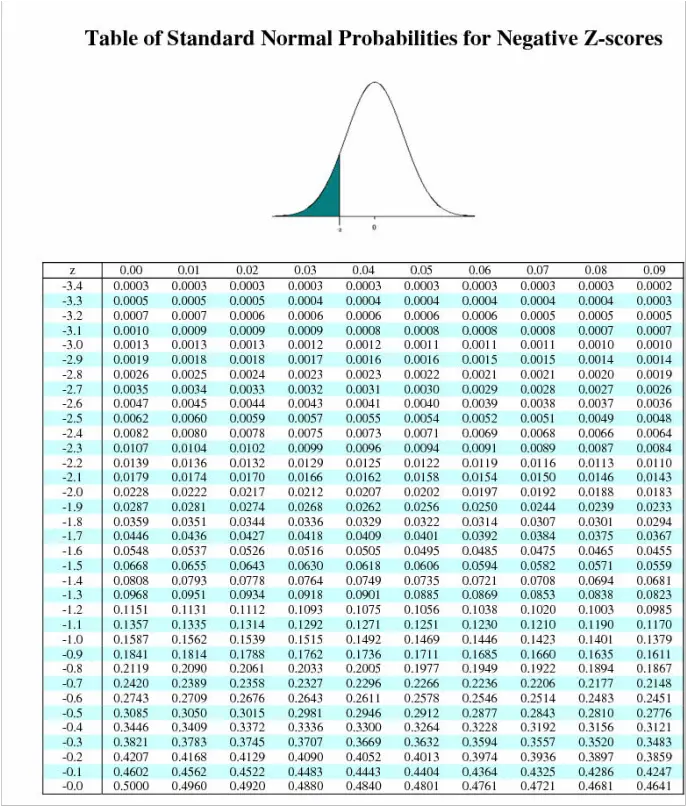
The Z score, also known as the standard score, measures how many standard deviations a data point is from the mean of a dataset. It is a crucial concept in statistics and probability, allowing you to understand the relative position of a data point within a distribution.
The Formula for Z Score
The formula for calculating the Z score is:
Z = (X – μ) / σ
- X is the value of the data point.
- μ is the mean of the dataset.
- σ is the standard deviation of the dataset.
This formula helps in determining how far and in what direction a data point deviates from the mean, making it easier to analyze and interpret data.
Why Use a Z Score Calculator?
Using a Z score calculator simplifies the process of determining the Z score of a data point. Here are some reasons why it is beneficial:
- Accuracy: Manual calculations can be prone to errors, especially when dealing with large datasets. A calculator ensures precision.
- Efficiency: It saves time by quickly computing the Z score, allowing you to focus on data analysis rather than calculations.
- Comparison: It facilitates the comparison of different datasets by standardizing data points.
- Outlier Detection: Z scores help in identifying outliers that can skew data interpretation.
How to Use a Z Score Calculator
Using a Z score calculator is straightforward. Here’s a step-by-step guide:
- Input the Data Point (X): Enter the value of the data point you wish to analyze.
- Enter the Mean (μ): Provide the mean of the dataset. This is the average value of all data points.
- Provide the Standard Deviation (σ): Enter the standard deviation, which measures the amount of variation or dispersion in the dataset.
- Calculate: Click on the calculate button to get the Z score.
The calculator will instantly provide the Z score, indicating how many standard deviations the data point is from the mean.
Applications of Z Score
The Z score has numerous applications across various fields:
- Finance: In finance, Z scores are used to assess the risk of investment portfolios and to identify overbought or oversold assets.
- Healthcare: In healthcare, Z scores help in evaluating patient data against population norms, such as in bone density tests.
- Education: In education, Z scores are used to compare student performance across different tests.
- Quality Control: In manufacturing, Z scores help in maintaining quality standards by identifying deviations from the norm.
Interpreting the Z Score
Interpreting the Z score is crucial for data analysis:
- Z Score = 0: The data point is exactly at the mean.
- Z Score > 0: The data point is above the mean.
- Z Score < 0: The data point is below the mean.
- Z Score > 2 or < -2: The data point is considered an outlier.
Understanding these interpretations helps in making informed decisions based on data analysis.
Advantages of Understanding Z Scores
Knowing how to calculate and interpret Z scores offers several advantages:
- Data Normalization: It allows for the normalization of data, making it easier to compare different datasets.
- Improved Analysis: It enhances the accuracy and depth of statistical analysis.
- Better Decision Making: With a clear understanding of data deviations, decision-making becomes more informed and reliable.
Common Mistakes to Avoid
While using a Z score calculator, it’s essential to avoid common mistakes:
- Incorrect Data Entry: Ensure that the data point, mean, and standard deviation are entered correctly.
- Misinterpretation: Understand the implications of the Z score to avoid incorrect conclusions.
- Overreliance: While Z scores are helpful, they should be used in conjunction with other statistical tools for a comprehensive analysis.
Mastering the use of a Z score calculator is an invaluable skill in the realm of statistics. It not only aids in the accurate analysis of data but also enhances your ability to make informed decisions. By understanding how to calculate and interpret Z scores, you can unlock deeper insights into your data, making you a more effective analyst or researcher. As you continue to explore the world of statistics, remember that the Z score calculator is a powerful ally in your analytical toolkit.